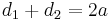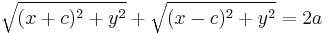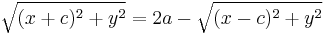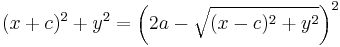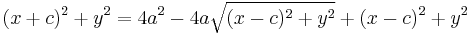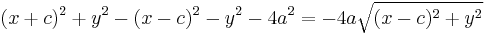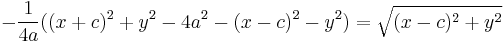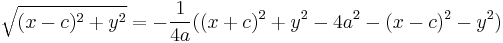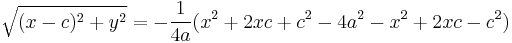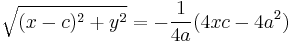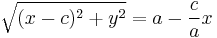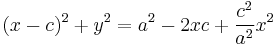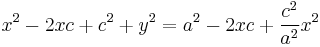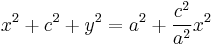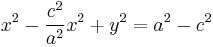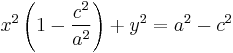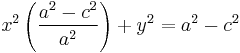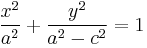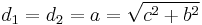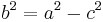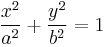Proofs involving the ellipse

The derivation of the cartesian form for an ellipse is simple and instructive. One simple definition of the ellipse is the "locus of all points of the plane whose distances to two fixed points(called the foci) add to the same constant". See ellipse for other definitions.

Let the foci be points (-c,0) and (c,0). Then the ellipse center is (0, 0).If (x,y) is any point on the ellipse and if 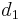$d_1$ is the distance between (x,y) and (-c,0) and 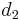$d_2$ is the distance between (x,y) and (c,0), i.e.

then we can define $a$

$d_1 %2B d_2 = 2a\,$

(a here is the semi-major axis, although this is irrelevant for the sake of the proof). From this simple definition we can derive the cartesian equation. Substituting:

$\sqrt {(x%2Bc)^2%2By^2} %2B \sqrt {(x-c)^2%2By^2} = 2a$

To simplify we isolate the radical and square both sides.

$\sqrt {(x%2Bc)^2%2By^2} = 2a - \sqrt {(x-c)^2%2By^2}$

$(x%2Bc)^2 %2B y^2 = \left ( 2a - \sqrt{(x-c)^2%2By^2} \right )^2$

$(x%2Bc)^2 %2B y^2 = 4a^2 - 4a\sqrt{(x-c)^2%2By^2} %2B (x-c)^2 %2By^2$

Solving for the root and simplifying:

$(x%2Bc)^2 %2B y^2 - (x-c)^2 - y^2 - 4a^2 = - 4a\sqrt{(x-c)^2%2By^2}$

$-{1 \over 4a}((x%2Bc)^2 %2B y^2 - 4a^2 - (x-c)^2 - y^2) = \sqrt{(x-c)^2%2By^2}$

Swap sides to return to original format and continue:

$\sqrt{(x-c)^2%2By^2} = -{1 \over 4a} ((x%2Bc)^2%2By^2-4a^2-(x-c)^2-y^2)$

$\sqrt{(x-c)^2%2By^2} = -{1 \over 4a} (x^2 %2B 2xc %2B c^2 -4a^2 -x^2 %2B2xc -c^2)$

$\sqrt{(x-c)^2%2By^2} = -{1 \over 4a} (4xc - 4a^2)$

$\sqrt{(x-c)^2%2By^2} = a - {c \over a}x$

A final squaring

$(x-c)^2%2By^2 = a^2 - 2xc %2B {c^2 \over a^2}x^2$

$x^2 - 2xc %2B c^2 %2B y^2 = a^2 -2xc %2B {c^2 \over a^2}x^2$

$x^2 %2B c^2 %2B y^2 = a^2 %2B {c^2 \over a^2}x^2$

Grouping the x-terms and dividing by 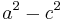$a^2-c^2\,$

$x^2 - {c^2 \over a^2}x^2 %2B y^2 = a^2 - c^2$

$x^2 \left( 1 - {c^2 \over a^2} \right) %2B y^2 = a^2 - c^2$

$x^2 \left( {a^2 - c^2 \over a^2} \right) %2B y^2 = a^2 - c^2$

${x^2 \over a^2} %2B {y^2 \over a^2-c^2} = 1$

If x = 0 then

$d_1 = d_2 = a = \sqrt {c^2%2Bb^2}$

(where b is the semi-minor axis)

Therefore we can substitute

$b^2 = a^2 - c^2\,$

And we have our desired equation:

${x^2 \over a^2} %2B {y^2 \over b^2} = 1$